Inhalt
Mondphase berechnen
Eigentlich ganz einfach, wenn man ein genaues und nicht zu lange in der Vergangenheit liegendes Vollmonddatum kennt. Man rechnet dann die Zeit seitdem bis heute aus und teilt das Ergebnis durch die Zeit, die zwischen zwei Neumondereignissen vergeht. Von diese Ergebnis verwenden wir nur den Teil hinter dem Komma und haben so die aktuelle Phase ermittelt.
Der Phasenwert liegt zwischen null und eins, und sagt folgendes aus:
- 0.0 bedeutet Vollmond
- 0.25 abnehmender Halbmond (das letzte Viertel)
- 0.5 Neumond
- 0.75 zunehmender Halbmond (erstes Viertel)
Zu kompliziert? Dann ein Beispiel:
- Heute ist der 16.12.2018, 12:00 Uhr
- Ein "historischer" Vollmond war z.B. am 25.09.2018 um 4 Uhr, 52 Minuten. Ich empfehle hier den möglichst letzten Vollmond heranzuziehen, da die Umlaufzeit des Mondes variiert. Nachschauen könnt ihr z.B. bei http://vollmond.info
- Dazwischen liegen ziemlich genau 82,24 Tage
- Diese Zahl teilen wir durch 29,53 (das ist die synodische Umlaufzeit des Mondes, also die Zeit von Neumond zu Neumond bzw. von Vollmond zu Vollmond.)
Als Ergebnis erhalten wir 2,785. - Die Zwei vor dem Komma bedeutet, dass inzwischen zwei Mondperioden durchlaufen wurden,
- die 0,785 nach dem Komma zeigt, dass wir einen zunehmenden Mond haben und es nicht mehr lang bis Vollmond ist – siehe Tabelle oben.
Disclaimer: Leider sind die Umlaufzeiten des Mondes alles andere als konstant. Insofern sollte der vergangene Vollmond nicht zu lange her sein, um ein möglichst genaues Ergebnis zu erzielen. Siehe auch Wikipedia.
In Python sieht das dann so aus – basierend auf der zur Ausführung geltenden Zeit:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#!/usr/bin/python #coding=UTF-8 import time now_time=time.mktime(time.localtime()) # constants syn_moon_month = 29.530589 # synodaler Monat # constants hist_fullmoon = 2018,9,25,6,1,36,0,0,1 # Historischer Vollmond als Strukturierte Zeit ---> Dies ist nur ein Beispiel ANPASSEN!! moon_time = time.mktime(hist_fullmoon) # Historischer Vollmond umgerechnet als Sekunden seit Epoch hist_fullmoon_days = moon_time/86400 # Historischer Vollmond - in Tagen seit Epoch # actuals now_days = now_time/86400 # Tage seit Epoch bis jetzt days_since_hist_fullmoon = now_days - hist_fullmoon_days # Differenz in Tagen: Jetzt - Historischer VM print days_since_hist_fullmoon full_moons_since = days_since_hist_fullmoon/syn_moon_month # Anzahl Vollmondereignisse seit hist. VM print full_moons_since phase = round(full_moons_since,2) # Abrunden auf 2 Nachkommastellen phase = (phase-int(phase)) # Nachkommastellen = Mondphase # calculate moon phase if phase == 0: phase=1 if phase < 0.25: ptext="abnehmender Mond (drittes Viertel)" elif phase == 0.25: ptext="abnehmender Halbmond (letztes Viertel)" elif 0.25 < phase < 0.50: ptext="abnehmende Sichel" elif phase == 0.50: ptext="Neumond" elif 0.50 < phase < 0.75: ptext="zunehmende Sichel" elif phase == 0.75: ptext="zunehmender Halbmond (erstes Viertel)" elif 0.75 < phase < 1: ptext="zunehmender Mond (zweites Viertel)" elif phase == 1: ptext = "Vollmond" print phase, ptext |
Aus Gründen der Nachvollziehbarkeit und zum Debuggen habe ich die einzelnen Rechenschritte nicht zusammengefasst. Epoch ist quasi der Nullpunkt der Unix/Linux Zeitrechnung und repräsentiert den 1.1.1970. Die Betriebssystem internen Zeitstempel basieren auf "Sekunden seit Epoch". Es gilt hier immer die eingestellte Systemzeit, also nicht UTC.
Einen vergangenen Vollmond könnt ihr für beliebige Orte der Welt auf der Seite mondverlauf.de nachschauen.
Das Abrunden auf 2 Nachkommastellen am Ende ist wichtig, da sonst nur für eine sehr kurze Zeit überhaupt die konkreten Phasen Voll, Halb und Neumond ausgegeben werden.
Beleuchtete Mondoberfläche
Will man nun ausrechnen, zu wieviel Prozent der Mond gerade beleuchtet wird, dann muss man etwas tiefer in die trigonometrische Trickkiste hinein greifen.
Etwas Mathematik
Da wir nur wissen wollen, wieviel Prozent der Mondscheibe sichtbar sind, müssen wir nicht wissen, wie groß der Mond an sich ist, es reicht die Annahme, dass die Mondscheibe von der Erde aus gesehen in etwa kreisförmig erscheint und dass die Trennlinie zwischen Hell und Dunkel (Terminator genannt) in etwa einer halben Ellipse gleicht. Für die Berechnung reicht uns daher als "Mondmodell" der sogenannte Einheitskreis mit Radius R = 1 und eine Ellipsenformel.
Ein Vollmond (entspricht 100% beleuchteter Mondoberfläche) hat in diesem Modell eine Fläche von 1² * π, also 3,1416. Ihr erinnert euch sicher noch: Die Fläche eines Kreises ist R²*π
Die Beleuchtung für alle Mondphasen dazwischen (also 0% für Neumond und 50% für Halbmond) berechnen wir, indem wir vom Halbmond ausgehen und die der Mondphase entsprechende halbe Ellipsenfläche abziehen oder addieren.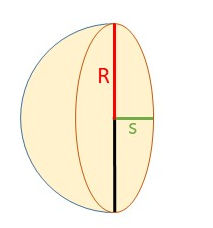
Die sichtbare Scheibe zwischen Halb und Vollmond errechnet sich aus der Fläche des Halbkreises plus der halben Ellipsenfläche.
Für eine Scheibe zwischen Neumond und Halbmond errechnen wir die Beleuchtung aus der Fläche des Halbkreises minus der halben Ellipsenfläche.
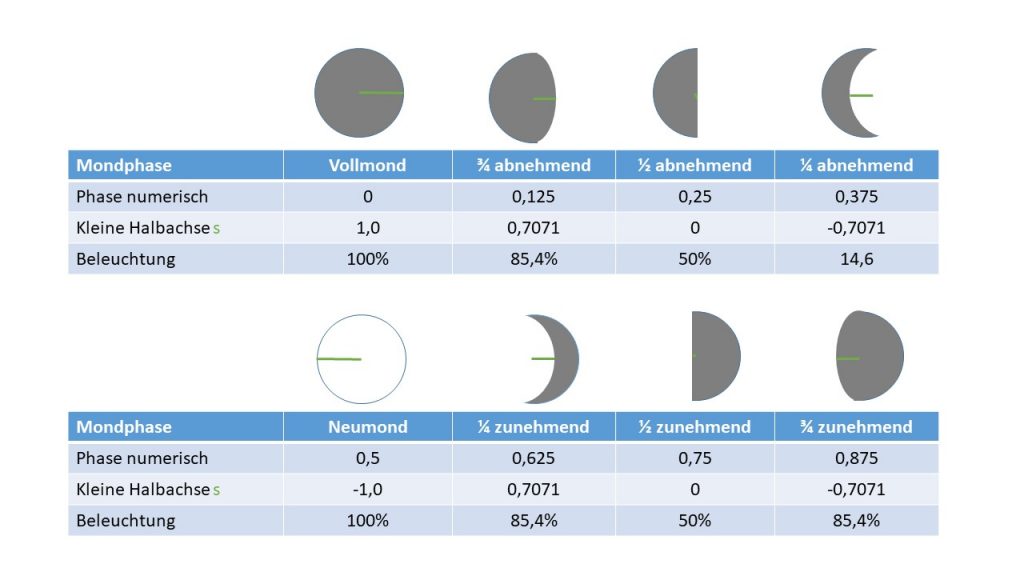
Die Fläche des Halbkreises beträgt π/2 also 1,5716.
Die Formel für die Fläche der Halbellipse lautet (s * R * π)/2
Die kurze Halbachse s errechnet sich unter Zuhilfenahme des weiter oben ausgerechneten Wertes phase.
Für Werte von phase zwischen 0 bis 0.5 lautet die Formel
s = cos(phase * 2 * π)
für Werte von phase zwischen 0.5 und 0.9999
s = – cos(phase * 2 * π)
(Minuszeichen vor dem cosinus beachten). Haben wir die Fläche der halben Ellipse berechnet, setzen wir das Ganze dann ins Verhältnis zum Vollkreis (Vollmond).
Ein Beispiel:
- Phase ist hier 0,375 (entspricht einem abnehmenden Viertelmond)
- s = cos(0,375 * 2 * π) = -0,7071
- Fläche der Ellipse = -0,7071 * 1 * π = -2,2214
- davon die Hälfte = -1,1107
- Addiert zur Fläche des Halbkreises = 1,5708 + (-1,1107) = 0,4601
- in Prozent des Vollkreises = 0,4601/3,1416 * 100 = 14,6% der Mondoberfläche sind beleuchtet.
Python Code
Auch hier habe ich die einzelnen Rechenschritte zum besseren Verständnis – und um das Debuggen zu erleichtern – nicht zusammengefasst.
Achtung: je länger der von euch im Code weiter oben gewählte Vollmondtermin her ist, desto ungenauer wird das Ergebnis.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#Beleuchtete Mondoberfläche in Prozent auf Basis der Phase berechnen from math import pi, cos #Konstanten phase = 0.375 # Diese Zeile nur zu Testzecken hmoonA = float(pi/2) # Fläche des Einheitskreises/2 (d.h. Radius = 1) # Rechenwerk if phase < 0.5: s = cos(phase * pi * 2) # Errechnung kurze Halbachse s der Ellipse ellipse = s * 1 * pi # Ellipsenfläche = Produkt der beiden Halbachsen * Pi hEllA = ellipse / 2 # halbe Ellipsenfläche illA = hmoonA + hEllA # Beleuchtete Mondoberfläche = Halbmondfläche plus halbe Ellipsenfläche else: s = -cos(phase * pi *2) # Errechnung kurze Halbachse s der Ellipse ellipse = s * 1 * pi # Ellipsenfläche = Produkt der beiden Halbachsen * Pi hEllA = ellipse / 2 # halbe Ellipsenfläche illA = hmoonA - hEllA # iBeleuchtete Mondoberfläche = Halbmondfläche plus halbe Ellipsenfläche illumperc = illA / pi * 100 # Beleuchtete Mondoberfläche in % der Vollmondoberfläche (Basis Einheitskreis mit r=1) illumperc = round(illumperc,1) # auf eine Nachkommestelle abrunden # Ausgabe print illumperc |
oder beides zusammen als Subroutine
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#!/usr/bin/python #coding=UTF-8 import time from math import pi, cos def moonphase(now_time): # constants syn_moon_month = 29.530589 # synodal length of moon cycle # constants hist_fullmoon = 2018,9,25,6,1,36,0,0,1 # base full-moon as struct time ---> adapt to most recent full-moon moon_time = time.mktime(hist_fullmoon) # base full-moon - seconds since epoch hist_fullmoon_days = moon_time/86400 # base full-moon - days since epoch now_days = now_time/86400 # days since eval days_since_hist_fullmoon = now_days - hist_fullmoon_days # difference in days between base fullmoon and now full_moons_since = days_since_hist_fullmoon/syn_moon_month # Number of full-moons that have passed since base full-moon phase = round(full_moons_since,2) # rounded to 2 digits phase = (phase-int(phase)) # trailing rest = % moon-phase # calculate moon phase if phase == 0: phase=1 if phase < 0.25: ptext="abnehmender Mond (drittes Viertel)" elif phase == 0.25: ptext="abnehmender Halbmond (letztes Viertel)" elif 0.25 < phase < 0.50: ptext="abnehmende Sichel" elif phase == 0.50: ptext="Neumond" elif 0.50 < phase < 0.75: ptext="zunehmende Sichel" elif phase == 0.75: ptext="zunehmender Halbmond (erstes Viertel)" elif 0.75 < phase < 1: ptext="zunehmender Mond (zweites Viertel)" elif phase == 1: ptext = "Vollmond" return phase, ptext def illumination(phase): #constants hmoonA = float(pi/2) # area of unit circle/2 # calculate percentage of moon illuminated if phase < 0.5: s = cos(phase * pi * 2) ellipse = s * 1 * pi # Ellipsenfäche = Produkt der beiden Halbachsen * Pi hEllA = ellipse / 2 # Ellipse Area/2 (major half axis * minor half axis * pi)/2 illA = hmoonA + hEllA # illuminated area of moon = Half moon area plus half Ellipse else: s = -cos(phase * pi *2) # minor half axis of ellipse ellipse = s * 1 * pi hEllA = ellipse / 2 # Ellipse Area/2 (major half axis * minor half axis)/2 illA = hmoonA - hEllA # illuminated area = Half moon area minus half Ellipse Area illumperc = illA / pi * 100 # illuminated area relative to full moon area (based on unit circle r=1) illumperc = round(illumperc,1) return illumperc if __name__ == '__main__': adesso = time.mktime(time.localtime()) mtupel = moonphase(adesso) mphase = mtupel[0] mphase_text = mtupel[1] millum = illumination(mtupel[0]) print "Phase numerisch: %1.2f, Mondphase: %s, beleuchtete Oberfläche %1.1f%%" % (mphase, mphase_text, millum) |
Wird das Programm direkt aufgerufen, gibt es die aktuelle Mondphase numerisch und in Textform sowie die beleuchtete Mondoberfläche aus.
Das Programm (ich habe es mond.py genannt) kann in andere Programme mit
import mond(ohne .py am Ende) eingebunden werden. Aufgerufen wird es folgendermaßen:
|
1 2 3 4 5 6 7 8 |
import time import mond #oder wie immer du dein Prog nennst # calculate moon phase and illumination jetzt = time.mktime(act_time) # Aktuelle Zeit mtupel = mond.moonphase(jetzt) # mond.mondphase(UnixZeitstempel) gibt ein Tupel aus: Element 0 = phase; Element 1 = Phasentext mphase = mtupel[1] # Phase als Text millum = mond.illumination(mtupel[0]) # mond.illumination(phase) gibt die beleuchtete Oberfläche aus |
Quellen:
Als sehr hilfreich zum Verständnis haben folgende Webseiten erwiesen:
http://www.Mondverlauf.de
http://avila.star-shine.ch/astro/berechnungen.html
Hi Christoph
Danke für das nette Programm :-).
Ich habe das nun hin und her getestet und komme immer zum selben Ergebnis, dass die Prozentausgabe meiner Meinung nach nicht korrekt ist.
Bspw. Heute 21.01.2024 11:00 Uhr müsste eigentlich die Pronzentangabe laut http://www.mondverlauf.de bei 81.6% liegen. Obiger Code gibt bei mir jedoch dann 76.8% aus.
Mach ich da etwas falsch? Bitte überprüfe mal deinen Code.
LG und Danke René
Hallo René,
danke für deinen Hinweis. Du hast recht… aber auch nicht. Die Formel stimmt, wenn du als Datum des "historischen" Vollmondes nicht den 25.09.2018 verwendest sondern möglichst den jeweils letzten Vollmond (per heute wäre das der 07.12.2023 um 01:33:12 Uhr).
Was ich beim Verfassen des Artikels in grauer Vorzeit nicht gewusst, bzw. erwähnt habe: Leider ist der Mondzyklus aufgrund der elliptischen Form seiner Umlaufbahn um die Erde nicht 100% regelmäßig. Außerdem spielt noch der Einfluss der Gravitation vor allem der Sonne aber auch von Jupiter und Saturn auf das Erde-/Mondsystem eine Rolle.
Zitat Wikipedia: "Die genannten Monatslängen sind Mittelwerte. Da die Bewegungen sowohl des Mondes als auch der Erde auf ihren elliptischen Bahnen ungleichförmig sind, können einzelne Monate mehr oder weniger stark davon abweichen. Die Dauer eines gegebenen synodischen Monats kann beispielsweise bis zu etwa 7 Stunden länger oder 6 Stunden kürzer sein als der mittlere synodische Monat.[14] Darüber hinaus unterliegen die mittleren Monatslängen aufgrund langfristiger Veränderungen der Erd- und Mondbahn einer langsamen Drift."
Ich werde einen Hinweis in den Beitrag aufnehmen.
Viele Grüße in die Schweiz
Chris
Danke, mit dem Vollmond-Datum vom 27.12.23 01:33 Uhr kommt die Prozentangabe doch ziemlich genau hin ;-).
LG René
Gibt es noch ein Verfahren, um die "Ungenauigkeiten" zu korrigieren?
Das ist eine schwierige Frage, da es jede Menge externer Einflussfaktoren gibt. Siehe auch meinen Kommentar zur fast gleichlautenden Frage. https://www.rustimation.eu/index.php/mondphase-und-beleuchtung-ausrechnen/comment-page-1/#comment-1986
War mir zu komplex, ich rechne einfach A = cos(2*pi*phase)*0,5+0,5
genau!
Ja, das gibt Fleißpunkte im Geometriekurs!